統計学を学ぼう

統計学とは、データを収集、整理、分析し、その結果から意思決定や予測を行う学問です。統計学は現代の社会、経済、科学、工学、医学など幅広い分野で活用されており、事実に基づいた判断を下すための重要なツールとなっています。

統計学はデータを収集、整理、分析し、その結果から意思決定や予測を行う学問とのことですが、よくわかりません。

統計学を総論的に概観し、5つの小見出しを通してその本質的な役割や基本概念について解説します。

統計学の基礎と重要性
データの収集と整理
確率と統計的推測
データ分析とモデル化
統計学の応用と課題

統計学の基礎と重要性

統計学の始まりは、人々がデータを体系的に理解し、パターンや傾向を見出す必要に迫られたことに起因します。古代では人口調査や税収データの管理などがその一例です。現代において統計学が重要視される理由は、膨大なデータが日々生み出されるデータ社会において、適切な判断を行うために不可欠な方法論を提供するためです。

統計学の基本は、大きく次の2つに分けられます。
• 記述統計（Descriptive Statistics）：データを要約し、わかりやすく提示する。
• 推測統計（Inferential Statistics）：サンプルデータから母集団に関する推定や予測を行う。

また、統計学は意思決定や問題解決に寄与するほか、ビジネス戦略や医療分野での治療効果判定などに応用されており、情報の信頼性と意思決定の正確性を高めます。

データの収集と整理

統計学における最初のステップはデータの収集と整理です。正確なデータがなければ分析結果は信頼できないため、データ収集には慎重さが求められます。データは以下のような形式で収集されることがあります。

• 定量データ（数値によって表されるデータ）
• 定性データ（カテゴリーや属性によるデータ）

データ収集の方法には調査、観察、実験、アンケートなどがあり、調査設計が重要です。また、データの整理には表形式やグラフを使い、視覚的に理解しやすい形にすることで次の分析段階へと進む準備が整います。

確率と統計的推測

統計学の重要な概念の1つが「確率」です。確率とは、特定の事象が発生する可能性を数値化したものです。確率は統計的推測において重要な役割を果たします。推測統計では、サンプルデータから母集団に関する推定を行うため、確率分布を活用します。

重要な確率概念の例

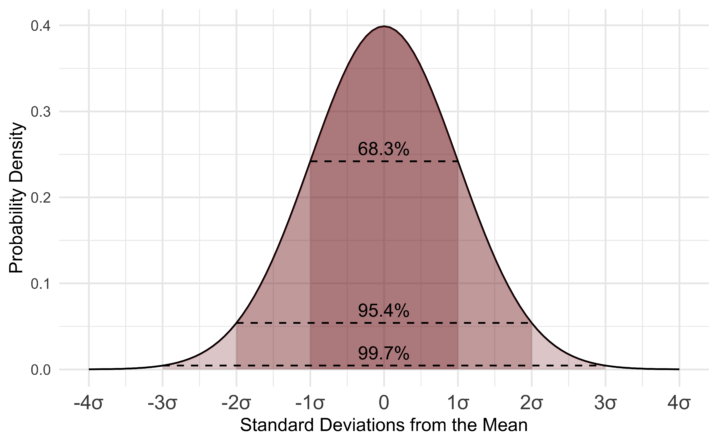
• 正規分布：多くの自然現象が従う分布で、平均を中心とした釣鐘型の形状。
• 信頼区間：母集団の真の値が一定の範囲に含まれる確率を示す。

また、統計的仮説検定は、ある仮説がデータに基づいて正しいかを判断するために用いられます。たとえば、治療効果があるかどうかを検証する場合などです。

データ分析とモデル化

統計学におけるデータ分析は、単なるデータの整理から一歩進み、問題解決や予測につながる意思決定をサポートします。分析には多様な手法があり、目的に応じて使い分けられます。

主な分析手法には以下のようなものがあります。

• 回帰分析：変数間の関係性をモデル化する手法。たとえば、気温がアイスクリームの売上にどう影響するかを調べる。
• 分散分析（ANOVA）：複数のグループ間で平均に差があるかを検定する。
• クラスタリング：データをいくつかのグループに分け、類似する特徴を持つもの同士をまとめる。

これらの分析に基づき、データの背後に潜むパターンや要因を明らかにし、事前の仮説の検証や新たな知見の発見につながります。

統計学の応用と課題

統計学は現実世界の多様な場面で活用されています。具体例としては以下のような分野があります。

• 医療分野：新薬の効果や治療法の有効性をデータに基づいて評価する。
• マーケティング：消費者行動を分析し、効果的な広告や商品戦略を立案する。
• 金融業界：リスク管理や投資パフォーマンスの最適化に活用される。

しかし、統計学の活用には課題も存在します。データの偏りやサンプルの選び方次第で、結果が大きく異なる場合があるため、分析の透明性や倫理が求められます。また、ビッグデータの登場により、従来の統計手法では対応しきれないケースも増えており、新しい技術やアルゴリズムの開発が進められています。

統計学の全体像を把握し、具体的な手法を学ぶための基盤を築くことが出来ました。

統計学は株式投資に応用することができますので、基本的な知識や計算手法を学んでおくと良いですよ。

まとめ

統計学は単なるデータ分析にとどまらず、現代社会において重要な意思決定や未来予測において不可欠な学問
データの正確な収集と分析、確率概念に基づいた推測、実際の応用までを包括的に理解することが重要
複雑化するデータ環境下では新しい課題に対応する柔軟性も必要
今後も統計学の進化は続き、さまざまな分野での応用がさらに拡大すると考えらる

著者プロフィール

K2編集部: 投資家、現役証券マン、現役保険マンの立場で記事を書いています。
K2アドバイザーによって内容確認した上で、K2公認の情報としてアップしています。